UMich TASP 2005: I can't get over how cool this is

Friday, March 17, 2006

I can't get over how cool this is

In one of my wikipedia-ing sessions, I came across a proof of e^pi*i=-1 that we can all understand, and it just struck me as being so incredibly cool (i'm not one to use the word "beautiful" outside of music, but this came close) so I thought I'd share it with everyone.
I don't know why e^pi*i=-1, but it's been proven, so it's true. Does anyone get this at all?

Define the complex number $z$ such that

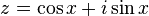$z=\cos x + i\sin x \,$ (ignoring the modulus term, as this cancels later)

Differentiating $z$ with respect to $x$ :

$\frac{dz}{dx}=-\sin x + i\cos x$

Using the fact that i² = -1:

$\frac{dz}{dx}=i^2\sin x + i\cos x=i(\cos x + i\sin x)=iz$

Separating variables and integrating both sides:

$\int\frac{1}{z}\,dz=\int i\,dx$

$\ln z=ix + C\,$

where

C

is the constant of integration.

To finish the proof we have to argue that $C$ is zero. This is easily done by substituting $x = 0$ .

$\ln z = C\,$

But $z$ is just equal to:

$z = \cos x + i\sin x = \cos 0 + i \sin 0 = 1 \,$

thus

$\ln 1 = C \,$

$C = 0 \,$

So now we just exponentiate

$\ln z = ix \,$

$e^{\ln z} = e^{ix} \,$

$z = e^{ix} \,$

$e^{ix} = \cos x + i\sin x \,$

Q.E.D.

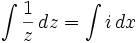
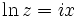
5 Comments:

Dylan said...

Hey. I gave my presentation for advanced topics in math on π, and proved that identity (e^(iπ)+1=0)!

Anyway, there's also a rigorous (and easy to understand) proof that uses the Taylor series for sin, cos, and e^x. But the beauty of the equation is that e, which we thought was just the great calculus constant, shows up in complex analysis (and geometry). Even more amazing is that the equation combines math's 5 most important constants (0, 1, i, e, and π) into a single equation, using the four most important operations (addition (+1), multiplication (iπ), exponentiation (e^(iπ)), and equality.

I could go on, but yeah, it's a great equation. It's also very important in chaos theory, because you use e^(ix) as a proxy for cis x, and it allows you better to analyze things like the Mandelbrot set that rely on functions of complex numbers.

10:31 PM, March 17, 2006

Sam said...

Sweet! I'm afraid my appreciation of it isn't quite as deep or refined as Dylan's, but a question came up about this in my Maths (grr . . . British people) mock exam, and I didn't know how to show this. Luckily, nobody expected me to know it, but I'm glad to get that sorted out. Thanks!

12:20 PM, March 18, 2006

Sanjukta said...